import pandas as pd
from pyndamics3 import Simulation
from pyndamics3.fit import fit, ParameterPopulating the interactive namespace from numpy and matplotlib
pyndamics3 version 0.0.29Populating the interactive namespace from numpy and matplotlib
pyndamics3 version 0.0.29sim=Simulation()
sim.add("y'= a*y*(1-y/k)",12,plot=True)
sim.params(a=0.3,k=100)
sim.add_data(t=x_data,y=y_data,plot=True)
sim.run(1995,2012)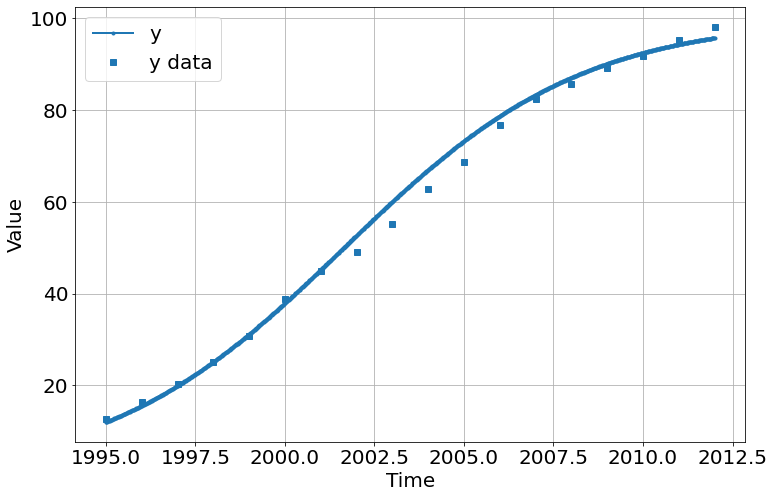
<Figure size 864x576 with 0 Axes>results=fit(sim,
Parameter("a",value=0.5,min=0),
Parameter("k",value=100,min=0),
)
sim.run(1995,2012)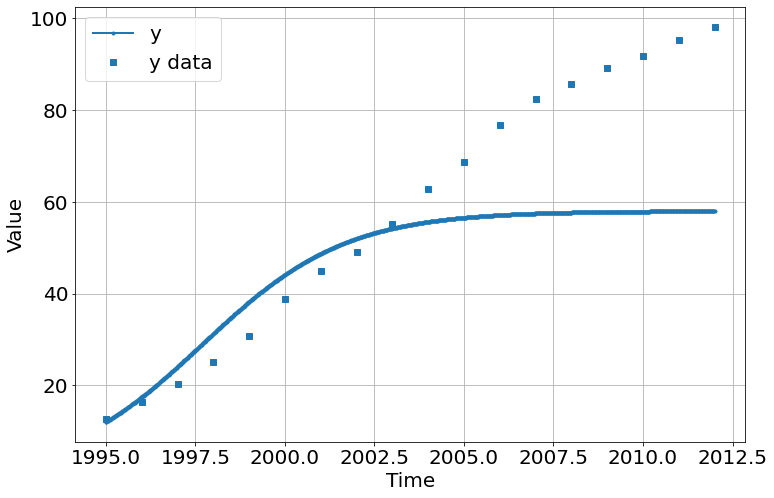
<Figure size 864x576 with 0 Axes>| fitting method | leastsq | |
| # function evals | 7 | |
| # data points | 18 | |
| # variables | 2 | |
| chi-square | 14627.1940 | |
| reduced chi-square | 914.199625 | |
| Akaike info crit. | 124.604787 | |
| Bayesian info crit. | 126.385530 |
| name | value | initial value | min | max | vary |
| a | 0.50000000 | 0.5 | 0.00000000 | inf | True |
| k | 58.0001111 | 100 | 0.00000000 | inf | True |
sim=Simulation()
sim.add("y'= a*y*(1-y/k)",12,plot=True)
sim.params(a=0.3,k=100)
sim.add_data(t=x_data,y=y_data,plot=True)
sim.run(20)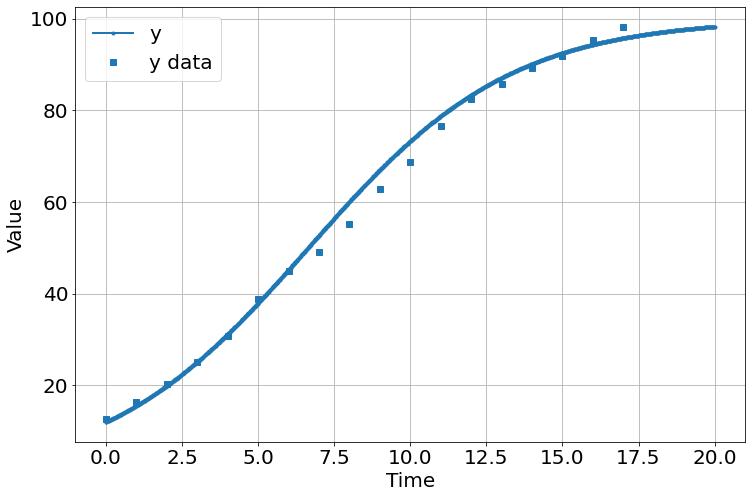
<Figure size 864x576 with 0 Axes>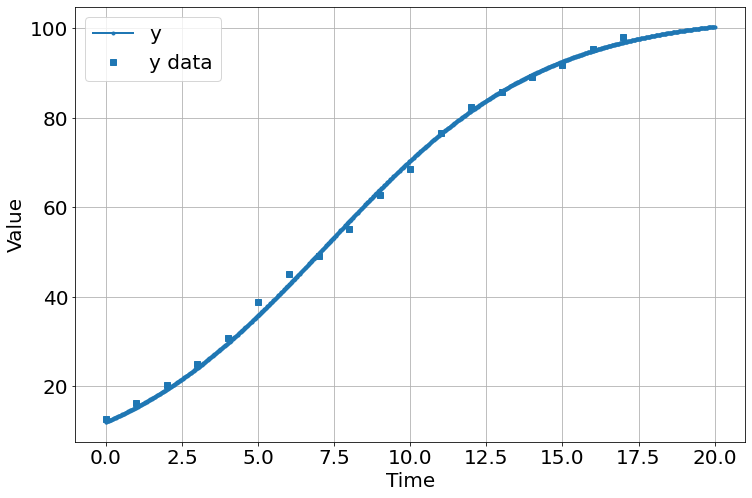
<Figure size 864x576 with 0 Axes>| fitting method | leastsq | |
| # function evals | 16 | |
| # data points | 18 | |
| # variables | 2 | |
| chi-square | 30.6986915 | |
| reduced chi-square | 1.91866822 | |
| Akaike info crit. | 13.6092689 | |
| Bayesian info crit. | 15.3900124 |
| name | value | standard error | relative error | initial value | min | max | vary |
| a | 0.27934262 | 0.00382039 | (1.37%) | 0.5 | 0.00000000 | inf | True |
| k | 103.234169 | 1.20806071 | (1.17%) | 100 | 0.00000000 | inf | True |
| a | k | -0.8281 |
results=fit(sim,
Parameter("a",value=1,min=0,max=20),
Parameter("initial_y",value=1,min=0),
Parameter("k",value=30,min=0),
)
results| fitting method | leastsq | |
| # function evals | 9 | |
| # data points | 18 | |
| # variables | 3 | |
| chi-square | 14627.1940 | |
| reduced chi-square | 975.146267 | |
| Akaike info crit. | 126.604787 | |
| Bayesian info crit. | 129.275902 |
| name | value | initial value | min | max | vary |
| a | 1.00000000 | 1 | 0.00000000 | 20.0000000 | True |
| initial_y | 1.00000000 | 1 | 0.00000000 | inf | True |
| k | 58.0001111 | 30 | 0.00000000 | inf | True |